Chapter 5. Introduction of Western Mathematics
Column Trigonometric Tables (Level 2)
The trigonometric functions originate from trigonometry, which deals with the relationships between the six types of ratios conceivable for a right triangle, and comprise six types of functions that relate the values of such ratios to an angle. The term trigonometry means surveying of a triangle. A precursor to the trigonometric functions could already be seen in ancient Egypt 4000 years ago, and their concept could also be seen in the astronomy of Babylonia and Greece. A book called Aryabhatiya written in India in the sixth century describes the method for calculating the sine values of various angles and clearly recognizes the concept as a type of a trigonometric function. It is thought that the trigonometric functions of India were transmitted to Europe via Arabia, and that the notations such as sin, cos, and tan that are used today were invented in Europe. They were transmitted to Japan through books related to mathematics and astronomy written in Dutch, and through Chinese translations of European mathematics and astronomy transmitted to China (in books such as Chongzhen lishu). They were chiefly used in astronomical calculations, surveying, and navigation, and frequently appeared in books related to physics in Europe. Since the trigonometric functions are correspondence between angles and numbers, they could not have been born without the concept of an angle. However, Wasan lacked the concept of an angle. Directions were indicated by relating them to the twelve horary signs, but as they were not quantified, intermediate directions could not be expressed accurately. Angles were only used in the fields of astronomy, surveying, and navigation.
The trigonometric tables are tables that lists the values of sine (sin), cosine (cos), and tangent (tan) for a given angle. Ptolemy (c.85-c.165) in the ancient Greece listed the sine values in Almagest. In more precise terms, the table is called a chord table, which lists chords two times the length of the side opposite to an angle (central angle), two times a given angle of a right triangle (circle) whose hypotenuse (radius) has a length of 60.
Figure for Showing the Relationships between the Chord Table and Trigonometric Functions
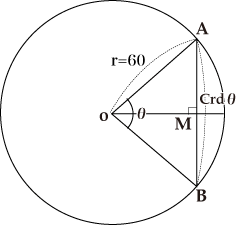 The Ptolemy (Ptolemaios) chord table lists Crdθ, the length of the chord AB that corresponds to ∠AOB, and it is calculated on the assumption of OA=OB=60. For example, we see values such as
The Ptolemy (Ptolemaios) chord table lists Crdθ, the length of the chord AB that corresponds to ∠AOB, and it is calculated on the assumption of OA=OB=60. For example, we see values such as
![]() in the table.
in the table.
On the other hand, as sin x is defined as sin∠AOM=AM when OA=1, there is a relation Crd θ=2×60 sin θ/2. It follows from Crd 60°=60 that 120 sin 30°=60 or
![]() ,
,
and from Crd 90°=84.85277... that 120 sin 45°=84.85277… or sin 45°=0.7071064….
We could derive the current sine table by halving each angle and dividing the length of each chord by 120 in the table. Ptolemy also described the calculation method used to create the table in Almagest, and started with angles such as 30°, 45°, and 60°, which were easy for calculation, and calculated values as the lengths of the sides of a regular pentagon and a regular decagon for 36° and 72°. Furthermore, he derived a formula with which the lengths of chords for the sum and remainder of two angles could be calculated, using a theorem called the Ptolemy's theorem, and a formula for calculating the length of the chord for an angle that is a half of a given angle(Lengths of Chords for Sum and Remainder of Angles). Then, the sine values for 12°, 6°, 3°, 1.5°, and so on can be calculated. Next, he showed that the sine value for 0.5° is greater than 2/3 times that for 0.75° and smaller than 4/3 times that for 0.375°, and proved these two values are the same by calculation. In this way, Ptolemy listed the length of each chord for central angles from 0° to 180° in units of 0.5°(therefore, sine values for 0° to 90° in units of 0.25°).
Looking at the value for a central angle of 120°, for example, in this table, it describes an interpolation that the chord length for a central angle of 120° is 103;55,23
![]() and it increases in increments of ;0,31,18 as the angle increases in increments of
and it increases in increments of ;0,31,18 as the angle increases in increments of ![]() .
What is interesting here is that the fraction part of the length is represented in the sexagesimal system, and the reason why the radius is set to 60 is that calculations may be simplified in the interpolation. For reference, the first decimal place was called partes minutae primae and the second decimal place was called partes minutae secundae in medieval Europe. Minutus is an adjective meaning “fractionized”. It is because of this that the first subdivision of time and angles is called a “minute,” and the second subdivision is called a “second.”
.
What is interesting here is that the fraction part of the length is represented in the sexagesimal system, and the reason why the radius is set to 60 is that calculations may be simplified in the interpolation. For reference, the first decimal place was called partes minutae primae and the second decimal place was called partes minutae secundae in medieval Europe. Minutus is an adjective meaning “fractionized”. It is because of this that the first subdivision of time and angles is called a “minute,” and the second subdivision is called a “second.”
Then, let’s calculate sin 60° using this table.As sin 60° is a half of the length of the chord for central angle 120° of a circle with a radius of 1, when dividing the length of a chord
![]()
by 120, we obtain
![]()
, and find that it is identical to ![]() .
.
In India, the side opposite to the angle (a half of the chord) was called “jya,” and it was transcribed and called “jaib” in the Arabian world. As this sound means “bay” in Arabic, the Latin word “sinus” for “bay” was used when the word was translated into Latin in the twelfth century. This way, research on trigonometry, in which a regular chord was called sinus or sine, began in Europe. Among others, astronomers earnestly studied trigonometry, and Johannes Muller (1436-1476), known as Regiomontanus, wrote the first textbook for trigonometry De triangulus omnimodis (completed in 1464) and published the first trigonometric tables Tabula directionum (1490). Opus palatinum by G. Rheticus (1514-1576), published in 1596, was a compilation of trigonometry and trigonometric tables, weighing in at more than 1,400 pages. It is said that Copernicus and Kepler had established revolutionary theories in astronomy by using trigonometric tables.
The first trigonometric tables in Japan are said to be Sanreki zakko by Takebe Katahiro (1664-1739). Takebe Katahiro, famous for calculating Pi, created a half chord table derived from calculating values of ![]() sin x in units of 1 degree, to eleven places of decimals, using the value of Pi. Takebe called one degree one gen, and as he calculated the values using a circle with a diameter of 1, the length of a half chord was
sin x in units of 1 degree, to eleven places of decimals, using the value of Pi. Takebe called one degree one gen, and as he calculated the values using a circle with a diameter of 1, the length of a half chord was ![]() sin x shaku. Takebe created a table as shown in the figure derived from calculating the length of an arc, a sagitta, and a half chord in units of 1 gen. This book was reproduced in Takebe Katahiro’s Sanreki zakko (1995) by Sato Ken’ichi.
sin x shaku. Takebe created a table as shown in the figure derived from calculating the length of an arc, a sagitta, and a half chord in units of 1 gen. This book was reproduced in Takebe Katahiro’s Sanreki zakko (1995) by Sato Ken’ichi.
-
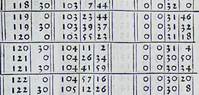
Values around Central Angle of 120° in the Chord Table in Units of 0.5°
Lager image for Ptolemy: Almagest
Ptolemy: Almagest (Venice, 1515)
Figure for Arc, Sagitta, and Half Chord by Takebe
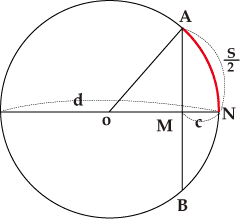 Takebe discovered the formula that finds a half arc (hanse)
Takebe discovered the formula that finds a half arc (hanse) ![]() from the diameter d and sagitta c, one that finds a sagitta from the half arc
from the diameter d and sagitta c, one that finds a sagitta from the half arc ![]() and the diameter d, and others. He also calculated that AM or the length of the half chord for angle 1° was 0.0087262032187, that for 2° was 0.0161679…, …, that for 30° was 0.25, that for 45° was 0.35355339…, that for 60° was 0.433012701…, and so on, on the assumption that the length of the arc for angle 1° was 0.00872664626 in a circle with a diameter of 1 shaku.
and the diameter d, and others. He also calculated that AM or the length of the half chord for angle 1° was 0.0087262032187, that for 2° was 0.0161679…, …, that for 30° was 0.25, that for 45° was 0.35355339…, that for 60° was 0.433012701…, and so on, on the assumption that the length of the arc for angle 1° was 0.00872664626 in a circle with a diameter of 1 shaku.
As these are the lengths of the half chords for a diameter of 1, the full chord (sine) is 2 times those values.
The trigonometric tables actually used in our country were the Chinese translations of trigonometric tables used in Europe and called Katsuen hassen hyo. Hassen means eight types of values shown in the figure, and the collective term of sine (sin x), cosine (cos x), ![]() ,
, ![]() ,
, ![]() ,
, ![]() , versine (1-cos x), and coversed sine (1-sin x).
, versine (1-cos x), and coversed sine (1-sin x).
Hassen
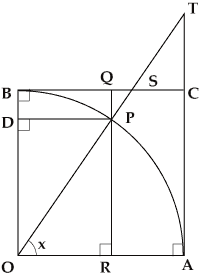 In the figure, assuming OA=OP=OB=radius=1,
In the figure, assuming OA=OP=OB=radius=1,
the following notation is defined:
Seigen (sine)=PR=sin x, Yogen (cosine)=DP=cos x
Seisetsu (tangent)=AT=tan x,
![]()
![]()
![]()
Seiya (versine)=RA=1-cos x, Yoya (coversed sine)=QP=1-sin x.
Then, we obtain sin2x+cos2x=1 by the Pythagorean theorem.
There are two types of table here, in which it is assumed that a right angle is 90 degrees: One table uses one minute derived by dividing one degree by 60, and another uses one minute derived by dividing one degree by 100. Katsuen hyo (1857) by Mori Masakado, as shown in the figure, takes one degree as 60 minutes, while Shinporekisho zokuhen (1846) by Shibukawa Kagesuke (1787-1856) takes one degree as 100 minutes.
The Katsuen hassen hyo is famous for the fact that Ino Tadataka (1745-1818), well-known to us for his cartography of Japan, carried it when surveying land. For information on the use of the trigonometric tables in surveying and cartography, please refer to the Column "Survey Methods".
As spherical trigonometry is used in astronomy, we find many multiplications of the trigonometric functions. A logarithm table for trigonometric functions was created to be used to convert the multiplications into additions, and that table was also imported and introduced to Japan. The trigonometric tables is required when solving transcendental equations such as sin x = ax+b, which appears when finding the length of a chord dividing a circle into three equal parts. As the trigonometric tables is now built into spreadsheets, the problem of dividing a circle into three equal parts can be simply solved using them.
-

Sine Values around 30 Degrees and Cosine Values around 60 Degrees
Lager image for Katsuen hyo
Mori Masakado: Katsuen hyo