Chapter 4. Wasan as a Practical Science
Column Survey Methods (Level 0)
Surveying has been applied as a method for calculating areas of the fields since ancient times. It has been also the technology indispensible for city planning and architecture, and astronomical observations and almanac creation. Geometry (Kikagaku) is a word coined from “geo” (meaning land) and “metry” (meaning surveying), indicating that surveying is a root of one field of mathematics. The word “Kika” was derived from the pronunciation of “geo” in Chinese during the translation of Elements by Euclid, the Father of geometry. In this section, we would like to explain basic surveying methods.
Land survey (Kenchi)
In the seventh century in Japan, as the “Land Allotment System” (Handen shuju no ho) was about to be put into force, they started to investigate the areas of rice fields based on a Chinese mathematical book Jiuzhang suanshu.
To measure areas, Chinese units such as bu, dan, and cho were used.
An area was found by measuring its component lengths and calculating them; it was also decided in ancient times that the area of a square having a side with a length of 6 shaku was 1 bu. For large areas, the units of 1 dan (360 bu) and 1 cho (10 dan) were also used, and the area of a square having a side with a length of 60 ken (360 shaku) was 1 cho. One cho was also used as a unit of length, 60 ken (360 shaku) was also called 1 cho; after the land survey by the Taiko (the title of the regent, given to Toyotomi Hideyoshi), the area of a square with a side of 1 cho was a little larger than one with a side of this 1 cho. As indicated by this example, we need to be careful when considering lengths in the past, because their standards and names changed from period to period. It was not decided that the length of 1 ken was 6 shaku; in some periods, 1 ken was 6 shaku 5 sun or 6 shaku 3 sun. One bu was also called 1 tsubo, and it was decided that 1 bu was an area of approximately 3.3m2based on the system of weights and measures in the Meiji Era. As 1 tsubo is the area of a square with sides of length 1 ken, 1 ken comes to approximately 1.8m. One shaku is one sixth of 1 ken or 30.3cm (to be exact, 1 shaku=10/33m).
By the way, Jiuzhang suanshu describes calculations of areas of rice fields in the beginning of Chapter 1 “Fang tian” (Rectangular fields); and it indicates computational formulae for the areas of “fang tian” (rectangular fields), “gui tian” (triangular fields), “ji tian” (right-angle trapezoidal fields), “yuan tian” (circular fields), “huan tian” (annular fields), and “hu tian” (fields of segments).
In the book, the value 3 is used for Pi. Jinkoki in Japan deals with areas in a chapter called “About land surveying,” which begins by converting units of areas. Then, it derives the area of a curved figure by approximating it with polygons, in addition to calculating areas such as those of regular triangles, regular hexagons, regular octagons, and parallelograms.
This method seems to be the one that was used in real land surveys. The area of a rice field is calculated by cruciately stretching ropes over the field to create rectangles whose areas are equal to that of the field. Kan’no kohonroku ge (1725) by Mao Tokiharu includes an illustration of how to stretch ropes over fields.
Regarding the areas of quadrilaterals far removed from rectangles, there is a method for calculating such an area by dividing a quadrilateral into two triangles, which is described in Sanyoki (c.1600), said to be the oldest existing mathematical book.
The area of a triangle can be calculated by measuring the lengths of the three sides and applying Heron’s formula to the results, but it seems that this method was not generally used. Regarding the area of a quadrangle, there is a method that uses a cut-to-fit operation explained in the Column "Pythagorean Theorem",which calculates the area after transforming the quadrangle into a rectangle.
-

Illustration of How to Cruciately Stretch Ropes
Lager image of Kan’no kohonroku ge
Kan’no kohonroku ge -
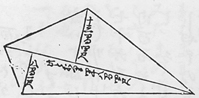
Figure for “Kenchi sao no uchiyo” (How poles for land survey should be laid)
Lager image of Sanyoki
Sanyoki
Height of a mountain
Now, the lengths of the sides of a land can be measured directly by some means such as ropes, but the heights of mountains cannot be measured directly. However, we know that the heights of mountains have been measured since ancient times. How did they measure the heights of mountains?
The mathematical book Jiuzhang suanshu in ancient China, previously mentioned, includes an example of finding the height of a mountain. The method explained in the book is to select a point that aligns with the top of a mountain and that of a tree in front the mountain, measure the distances to the tree and to the mountain from the point, and calculate the height of the mountain by using the similarity of the right triangles.
How to Measure the Height of a Mountain
In this figure, the tree top aligns with the mountain peak along the line of sight of the person.
If we know the lengths of DE, QE, BD, and AE, we can find the lengths of PR and PS by calculation because △ABC, △BPR, and △APS are similar.
In Japan also, the heights of mountains have been measured since ancient times, and although it does not describe survey methods, Izumo fudoki states that “Kan’nabi-yama is located 9 ri and 40 bu to the north east of Kooge. The mountain has a height of 230 jo and a circumference of 14 ri” and that “Ashibi-yama has a height of 170 jo…, and Ashikoya-san has a height of 180 jo….” These mountains are the present day Asahi-yama, Kyozuka-yama, and Hongu-san in Matsue City of Shimane Prefecture, and their heights are 342 m, 315 m, and 279 m respectively.We assume that they were measured with a surveying method introduced from China and we can imagine that as the heights of Kyozuka-yama and Hongu-san were inverse, the method included a major error.
Using an instrument called Shiho no kane (four sides measure) enabled the measurement of mountain’s height from any location.
This instrument has a weight hanging with a string from one apex on a square board, and each of the sides of the square board the weight hangs is marked with scales for length; when measuring the height of an object, the measurer directs and inclines one side toward the object, and reads the scale mark for the position of the string. Bundo yojutsu, written in the thirteenth year of Kyoho (1728) by Matsumiya Kanzan, illustrates how the instrument was used.
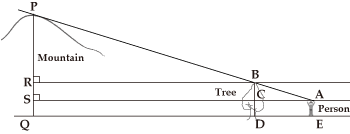
Even if one does not know the distance to a mountain, one can calculate the distance to the position directly under the summit of the mountain by performing measurements with this instrument on two points in the line that passes through the position.
Case where the Distance to a Mountain Is Unknown
In the figure, let the square ABCD be Shiho no kane having four sides whose lengths are 1.
If we measure the scale mark a at location M and the scale mark b at location N, and measure the distance c between M and N, we can find the length of PQ through calculation by using the fact that △MPQ and △BCE are similar, and △NPQ and △B’C’E’ are also similar. The formula is PQ=ab/(b-a)×c.
In those days (1727), the height of Mt. Fuji was measured, producing a result of approximately 3,886 m in terms of the metric system (today, the height is calculated as 3,776m).
Plane-table surveying
For surveying, there was a technique called Komoryu (Komo means red hair and ryu means a school) because it was introduced by Dutch.
The technique that was learnt in the middle of the seventeenth century by Higuchi Gon’emon (Kobayashi Yoshinobu), a yoriki (similar to a present-day police investigator) in Nagasaki from Caspar, a medical doctor. It was subsequenty passed down, and Shimizu Teitoku (1645-1717) systemized it as Kikujutsu.
Ki means a compass and ku means a ruler; and the technique involves drawing figures on a sheet of paper placed on a flat board, and performing calculations based on the figures. Books such as Bundo yojutsu by Matsumiya Kanzan, Kiku yoho kuden shiroku by Kawahara Sadayori, and Hiden chiiki zuho taizen by Hosoi Kotaku in the “Wasan Library” include descriptions of the specific method of this Komoryu surveying.
In this section, we would like to explain a method for measuring the distance to a point across a river.
Measuring Distance to a Point across a River
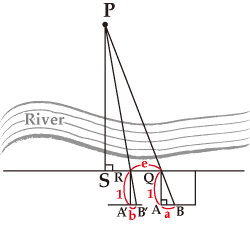
If, in the figure, we place Shiho no kane horizontally and draw △QAB at location Q, and then move along a line parallel to the segment AB to draw △RA’B’ at location R, we can calculate the distance to location P when we find the lengths of QR, QA, AB, RA’ and A’B’.
Assuming QA=RA’=1, AB=a, A’B’=b, and QR=c, We obtain ![]() .
.
If we move to location S and measure the length d of QS, specifically, we obtain ![]() .
.
Using the trigonometric tables
In the eighteenth century, devices for measuring angles and trigonometric tables were introduced to Japan. This introduction began the full application of Western-style surveying, and Kikujutsu described above also described methods for measuring angles and calculating a distance with a trigonometric table using the measured angles. If angles are used to measure the height of a mountain, the calculation method would be as follows:
Calculating the Height of a Mountain Using Trigonometric Functions
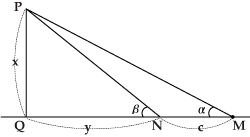
In the figure, let the measurement results be ∠PMQ=α, ∠PNQ=β, and MN=c.
Assuming PQ=x and QN=y, we obtain
![]() , using
, using
![]() .
.
That is, as it follows that
![]() ,
,
we can calculate the height of the mountain.
To make a survey of the distance to a point across the river, select two points, which are not necessarily in positions to make up a right triangle, and measure the distance between the two points, and each angle between each of the two points and the target point, and we can calculate the distance between each point and the target point as described in the following figure:
Triangular Surveying
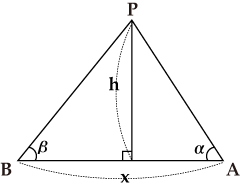
In the figure, let the measurement results be ∠PAB=α, ∠PBA=β, and AB=x. Then, using
x=PA cos α+PB cos β, and h=PA sin α=PB sin β, we obtain
![]() . So,
. So,
![]() . Similarly, as we obtain
. Similarly, as we obtain
![]() , and we can calculate the lengths of PA and PB.
, and we can calculate the lengths of PA and PB.
This is the principle of triangular surveying,and as it only requires one time measurement of a distance, triangulation points were set as reference points across the country in the Meiji era.
Making maps
A map can be made by repeated surveying. Kokuzu keiyo by Miyai Yasuhiro in the Wasan Library is a survey manual for cartography. Ino Tadataka (1745-1818) was a famous cartographer who surveyed lands with a technique called the graphical traversing method and drew the exact curves of coast lines and roads in maps.
Graphical Traversing Method
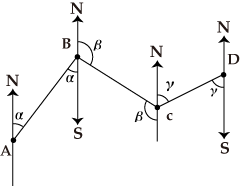
In the figure, a surveying method for moving forward as the surveyor measures the distance of AB and the angle α, that of BC and the angle β, and that of CD and the angle γ, and so on is called the Graphical Traversing Method. As ∠ABC=π+α-β, the distance of AC is found, and ∠BAC or ∠BCA can be calculated.
However, measuring distances involves great errors, and angles can be measured more accurately. So, triangular surveying uses ∠BAC, ∠ABC and the distance of AB to find the distance of BC or AC.
He improved his surveying method with various gems of ingenuity to reduce errors. He used quadrants to measure the altitude of the Pole Star to find the latitude of where he was, and used it for correction. As slopes tend to be measured longer than they really are, he measured gradients with a small quadrant and converted the lengths of slopes to those on a plane with a trigonometric table. The completed "Dainihon enkai yochi zenzu" was so accurate that it was used even in the Meiji era.
-

Bundo yojutsu
Library for Bundo yojutsu
NDL Digital Collections