Chapter 5. Introduction of Western Mathematics
Column Lengths of Chords for Sum and Remainder of Angles (Level 2)
Ptolemy calculated the lengths of chords for the sums and remainders of angles. With the lengths of the chords for two given angles, we can calculate the lengths of the chords for the sum and remainder of the two angles by using the Ptolemy's theorem (Ptolemy is the English form of Ptolemaios). Here, let’s prove the formula with the method described in Almagest.
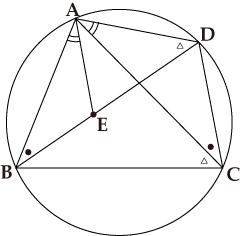
Ptolemy’s Theorem
Choose the point E on BD in the figure such that ∠BAE=∠CAD. As △ABE and △ACD are similar because their two angles are equal, it follows that AB/BE=AC/CD or AB×CD=AC×BE. Similarly, as the two angles of △ABC are equal to those of △AED, they are similar, and therefore it follows that AD/DE=AC/BC or AD×BC=AC×DE. If we add both the sides of the former equation to those of the latter equation, it follows that AB×CD+AD×BC=AC×(BE+DE)=AC×BD. Particularly, if the quadrangle ABCD is a rectangle such that AB=CD, AD=BC, ∠DAB=∠ABC=∠BCD=∠CDA=90°, it follows that AB×CD+AD×BC=AC×BD, which is equivalent to the Pythagorean Theorem.
If we let BC be a diameter of length 2R under this formula AC×BD=AB×CD+AD×BC, we obtain Crd(α)×Crd(180°-β)=2R×Crd(α-β) + Crdβ×Crd(180°-α) , and therefore we obtain the following formula, with which we can calculate the length of the chord for the remainder of the two angles:
Crd(α-β) = Crd(α)×Crd(180°-β)/2R - Crdβ×Crd(180°-α)/2R
This means an addition theorem of the trigonometric functions sin(x-y)=sin x×cos y-cos x×sin y from the relation of sin x=Crd(2x)/2R.
For the length of the chord for the sum of two angles, if we use Figure B, we obtain the following formula:
Crd(180°-α-β) = Crd(180°-α)×Crd(180°-β)/2R - Crdα×Crdβ/2R
This means cos(x+y)=cos x×cos y-sin x×sin y.
Length of the Chord for the Remainder of Two Angles
- Figure A
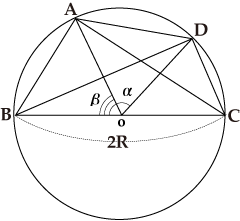 In the figure, we represent the length of the chord BD for ∠BOD=α with Crd α.
In the figure, we represent the length of the chord BD for ∠BOD=α with Crd α.
Assuming ∠AOB=β, as ∠AOC=180°-β holds true, we obtain AC=Crd(180°-β).
As ∠AOD=α-β, we obtain AD=Crd(α-β).
As ∠DOC=180°-α, we obtain DC=Crd(180°-α).
Length of the Chord for the Sum of Two Angles
- Figure B
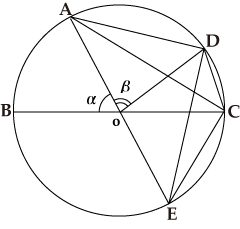 In the figure, assuming ∠AOB=α, as ∠AOC=180°-α holds true, we obtain AC=Crd(180°-α).
In the figure, assuming ∠AOB=α, as ∠AOC=180°-α holds true, we obtain AC=Crd(180°-α).
Assuming ∠AOD=β, as ∠DOE=180°-β holds true, we obtain DE=Crd(180°-β).
As ∠DOC=180°-α-β and ∠COE=α hold true, we obtain DC=Crd(180°-α-β) and CE=Crd α, and we use the Ptolemy’s theorem in conjunction with AD=Crd β.