Chapter 4. Wasan as a Practical Science
Column Pythagorean Theorem (Level 2)
The relation a2+b2=c2 with respect to the three sides of a right triangle is called the Pythagorean Theorem. This theorem has been known since ancient times as the name indicates; and we are not sure whether there is conclusive evidence that Pythagoras (c.BC570-c.BC500) really discovered it.
Pythagorean Theorem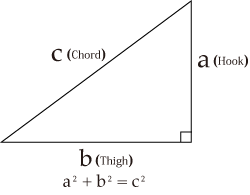
In the third century, Diogenes Laertios wrote in Philosophon bioi (Lives of eminent philosophers) that "According to Apollodoros, an arithmetician, it is said that when he discovered that the area of the square on the hypotenuse of a right triangle equals the sum of the areas of the two squares on the other two sides containing the right angle, he sacrificed a hundred bulls." However, we do not know any details about this arithmetician Apollodoros.
In the third century BC, Euclid proved the Pythagorean Theorem in his Stoikheia (Elements), in which he did not mention the name of Pythagoras. However, in A Commentary on the first book of Euclid Elementswritten by Proklos in the fifth century, and in De architectura written by Vitruvius, a Roman architect, in the first century BC, it is stated that the discoverer of this theorem was Pythagoras. These ancient documents were discovered in the Renaissance period, and since then, it has been included in Elements by Euclid that this theorem was in fact discovered by Pythagoras. However, the most dominant current opinion is that Pythagoras was not the discoverer of the theorem.
This theorem was called the law of Koukogen in Chinese mathematics, and was discussed in the ancient mathematical books Zhoubi suanjing and Jiuzhang suanshu.
Even after the theorem was introduced to Japan, the name Koukogen was used at it was.
Kou (hook) is a "right-angled hook," meaning two short sides containing a right angle; Ko (thigh) is a "leg joint," meaning a long side; and Gen (chord) is a "bowstring," meaning a hypotenuse.
This theorem was also discovered in ancient Babylonia and ancient India, and regarded as an important theorem used in surveying, architecture, astronomical observations, etc. The trigonometric functions are also closely related to the Pythagorean Theorem.
"Bowstring" in a Commentary to Zhoubi suanjing
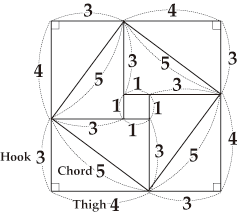 This commentary explains with a figure that 32+42=52holds true for a right triangle with three sides of lengths 3, 4, and 5, and this figure can help us to prove that a2+b2=c2 also holds true when the lengths are a, b, and c. Please look at the following two figures:
This commentary explains with a figure that 32+42=52holds true for a right triangle with three sides of lengths 3, 4, and 5, and this figure can help us to prove that a2+b2=c2 also holds true when the lengths are a, b, and c. Please look at the following two figures:
It is known to us that there are a few hundred methods for proving the Pythagorean Theorem. The method adopted by Euclid to prove the theorem is to use congruent triangles and equivalent deformation; in addition to this, we know an algebraic method using similarity; a method to prove the theorem from placing the same four right triangles in appropriate locations and calculating those triangles; and one that involves creating two squares on the two sides containing the right angle, decomposing the squares, and imposing them on the square on the hypotenuse.
Laying the Same Four Right Triangles
- In Figure 1
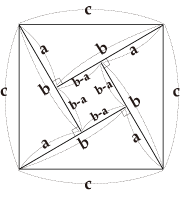 In Figure 1, it follows that c2=4・ab/2+(b-a)2
In Figure 1, it follows that c2=4・ab/2+(b-a)2
=2ab+b2-2ab+a2
=a2+b2- In Figure 2
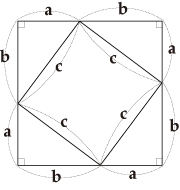 In Figure 2, it follows that c2=(a+b)2-4・ab/2
In Figure 2, it follows that c2=(a+b)2-4・ab/2
=a2+2ab+b2-2ab
=a2+b2
These proof methods using areas are related to the Bolyai-Gerwien theorem, and in Wasan, they were dealt with as cut-to-fit problems (which will be explained later ). Books that collect the methods of proving the Pythagoras Theorem include The Pythagorean proposition (Washington, D. C., 1968) by E.L.Loomis,which we can read at the electronic library ( http://www.eric.ed.gov/) provided by ERIC (Education Research Information Center) in the United States.
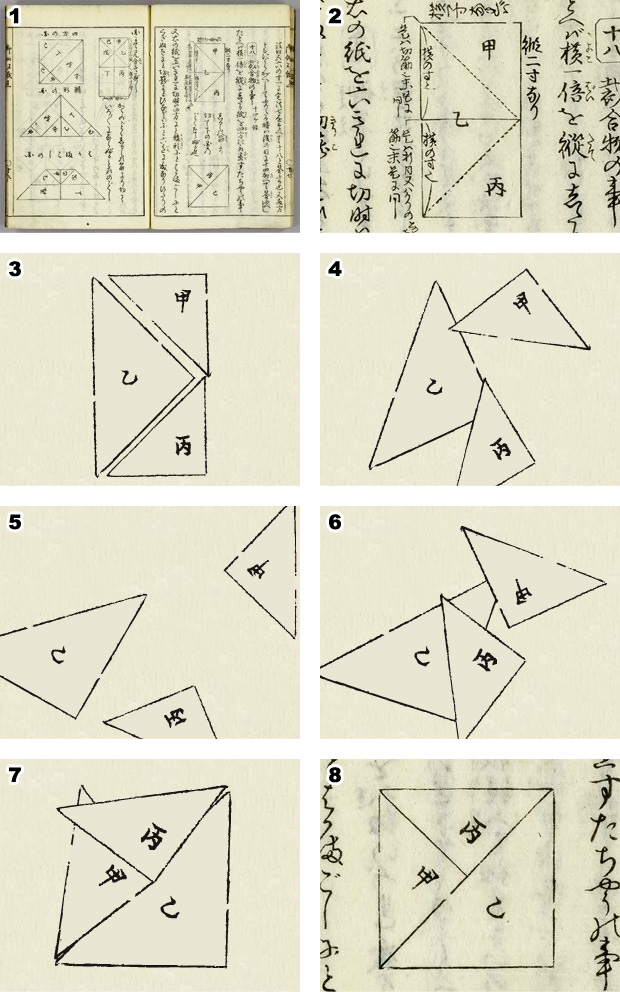
Example of Cut to Fit (from Kanja otogi zoshi)
Pythagorean triple
The triple (a,b,c) consisting of three natural numbers satisfying a2 + b2 = c2 is called the Pythagorean triple, and right triangles whose three sides are lengths a, b and c are called Pythagorean triangles. The most well-known Pythagorean triple is (3,4,5), while other Pythagorean triples include (5,12,13) and (15,8,17), etc.
We know that there are infinite number of Pythagorean triples; let's consider the reason for this. When we assume that n is any natural number and calculate
a2 + b2 for a=3n, b=4n, we obtain (3n)2+(4n)2=25n2=(5n)2.
Then, if we assume c=5n, (a,b,c) is a Pythagorean triple. Since n is any natural number, we can be certain that there are an infinite number of Pythagorean triples.
When we assume n=1,2,3..., we obtain the Pythagorean triples like (3,4,5)(6,8,10)(9,12,15)...
However, this method does not enable us to obtain the Pythagorean triple (5,12,13)with any n.
In fact, (5,12,13) is a special case where n=2 when assuming a=2n+1, b=2n(n+1), and c=2n2+2n+1; for any natural number n,
(2n+1)2+{2n(n+1)}2=4n4+8n3+8n2+4n+1=(2n2+2n+1)2 holds true, and therefore we know that (a,b,c) is a Pythagorean triple.
When we assume n=1,2,3..., we obtain Pythagorean triples like (3,4,5)(5,12,13)(7,24,25)...We can also discover this with the properties of quadrangular numbers as follows:
Quadrangular number and Pythagorean triple
If we keep adding odd numbers sequentially, we obtain square numbers (quadrangular numbers) like 1=12,1+3=22,1+3+5=32, and so on.
Sum of Odd Numbers Is a Square Number
 From the figure, we understand that 1+3=22, 1+3+5=32 , 1+3+5+7=42,・・・and so on hold true.
Represent the sum of the first n odd numbers with the following two ways:
S= 1 + 3 + 5 +......+(2n-3)+(2n-1)
From the figure, we understand that 1+3=22, 1+3+5=32 , 1+3+5+7=42,・・・and so on hold true.
Represent the sum of the first n odd numbers with the following two ways:
S= 1 + 3 + 5 +......+(2n-3)+(2n-1)
S=(2n-1)+(2n-3)+(2n-5)+......+ 3 + 1
Add the above two expressions:
2S= 2n + 2n + 2n +......+ 2n + 2n
Finally, we obtain S=n2
As indicated by the figure, 1+3+5+・・・+(2n?1)=n2 holds true. Using this relation, we can find a type of Pythagorean triples.
From 42=1+3+5+7 and 52=1+3+5+7+9=42+32, (3,4,5) is a Pythagorean triple.
From 122=1+3+5+・・・+23 and 132=1+3+5+・・・+23+25=122+52, (5,12,13) is a Pythagorean triple.
From 242=1+3+5+・・・+47 and 252=1+3+5+・・・+47+49=242+72, (7,24,25) is a Pythagorean triple.
When the last added odd number is itself a square number, sum of the odd numbers up to the last-but-one odd number is also a square number and their sum will also be a square number, so the three numbers are a Pythagorean triple.
Representing the last added odd number with (2p+1)2 as the square number and assuming that the quadrangle numbers are (n?1)2=1+3+5+・・・+(2n?3) and n 2=1+3+5+・・・+(2n?3)+(2p+1)2,
we obtain n=2p2+2p+1 and n?1=2p2+2p=2p(p+1) from 2n=4p2+4p+2 because (2p+1) 2=n2?(n?1)2=2n?1.
Therefore, (2p+1, 2p(p+1), 2p2+2p+1) for any natural number p is a Pythagorean triple.
Pythagorean triples in Wasan
However, (15,8,17) cannot be obtained with any of the above methods. Then, how can we find every Pythagorean triple exhaustively? Here, we would like to introduce the method described in Sanpo tenzan shinanroku (1815) by Sakabe Kohan (1759-1824).
First, he assumed that Kou (Hook) =2n(n+1),Ko (Thigh) =2n+1,Gen (Chord)=2n2+2n+1 are a Pythagorean triple as a latitudinal solution. He called nthe Class (Kyu). This is exactly the same as the previous result. Next, he performed horizontal calculations, the longitudinal solution for each Class with respect to parameters called Ta and Sho.
When Class=1, Sho is 1 and Ta increases with increments of 2 as follows: 2,4,6,8,10...; and when representing Ta with p, Hook=2p, Thigh=p2?1, Chord=p2+1 is a Pythagorean triple; (8,15,17) is the Pythagorean triple when p=4.
When Class=2, Sho is 2 and Ta increases with increments of 2, as 3,5,7,9,11...; and when representing Ta with p, Hook=4p, Thigh=p2?4, Chord=p2+4 is a Pythagorean triple.
When Class=3, Sho is 3 and Ta increases with increments of 2 as follows: 4,6,8,10,12...; and when representing Ta with p, Hook=6p, Thigh=p2?9, Chord=p2+9 is a Pythagorean triple.
Generally, when Class=n, Sho is n and Ta increases with increments of 2, as n+1,n+3,n+5,n+7,n+9; and when representing Ta with n+r (r=1,3,5,7,???), Hook=2n(n+r), Thigh=(n+r)2?n2, Chord=(n+r)2+n2 is a Pythagorean triple. This is the same solution as Hook=2mn, Thigh=m2?n2, Chord=m2+n2 found in the current textbooks, and every Pythagorean triple can be obtained with this method.
In Wasan, Pythagorean triples were sought with various methods in addition to this one.
Cut to fit
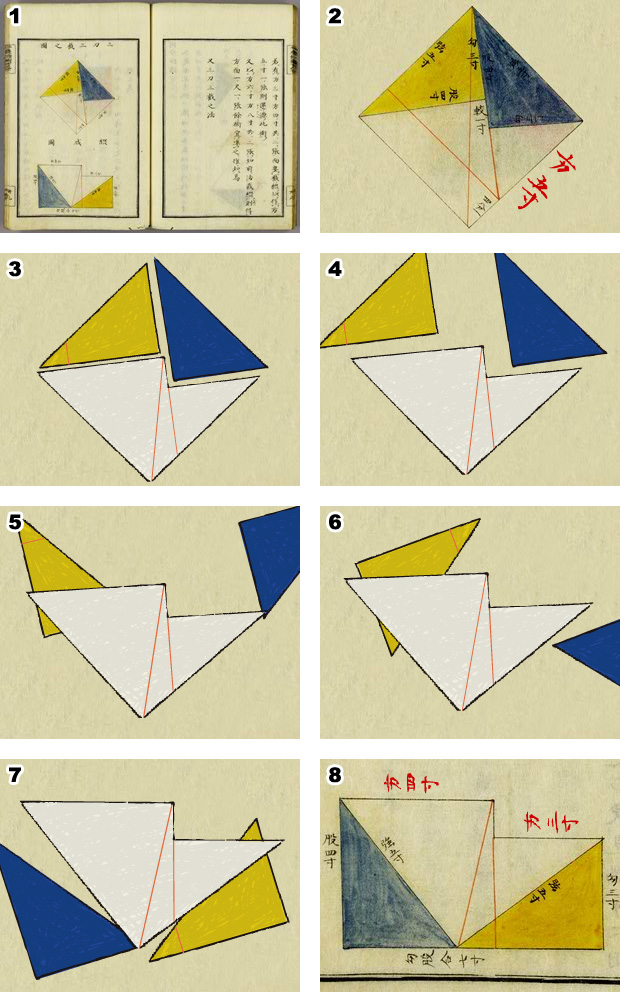
Example of Cut-to-Fit in Bundo yojutsu A square with sides of 5 sun (1 sun = 3.03cm) is divided into two squares with sides of 4 sun and 3 sun respectively.
One method for proving the Pythagorean Theorem is to show that one can cut two squares with a pair of scissors, and lay them again so that they are exactly overlaid on a different third square. More generally, when we cut a polygon with a pair of scissors, place the cut pieces in an arrangement to create a geometric shape with the same area as that of the original polygon, the action is called cut-to-fit. First, let's look at an example of a cut-to-fit operation to be regarded as a proof of the Pythagorean Theorem.
Proof of the Pythagorean Theorem with Cut to Fit Operation
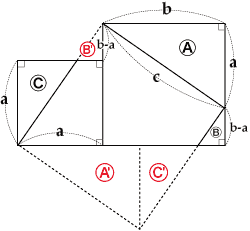 Here, we omit trying to prove this; and in the figure, the right triangle A and the right triangle A', the right triangle B and the right triangle B', and the right triangle C and the right triangle C' are congruent, and when we transpose C, A and B to C',A', and B', we obtain a square with sides of lengths c. This indicates a2+b2=c2; thus it is one proof of the Pythagorean theorem.
Here, we omit trying to prove this; and in the figure, the right triangle A and the right triangle A', the right triangle B and the right triangle B', and the right triangle C and the right triangle C' are congruent, and when we transpose C, A and B to C',A', and B', we obtain a square with sides of lengths c. This indicates a2+b2=c2; thus it is one proof of the Pythagorean theorem.
As indicated in the figure, we can cut two squares having sides of length a and length b respectively, and overlay them exactly on a square on a hypotenuse of length c.
In fact, there is a theorem that "If we have two polygons with the same area, we can create a polygon that is congruent to another polygon by dividing the former a finite number of times and rearranging the resultant pieces," and we also know that there are many ways to cut a polygon.
This theorem is called the Bolyai-Gerwien theorem and was discovered in 1833.
In Wasan, methods were investigated such as those for creating one square by cutting and fitting together three or five squares with the same area.
Similarly in three dimensions, it was questioned whether one could divide a tetrahedron and create a cube with the same volume as the tetrahedron, using the divided pieces. M. W. Dehn (1878-1952) proved in 1901 that it was impossible.
Heronian triple
When the lengths of the three sides of a triangle are natural numbers and its area is also a natural number, the triangle is called a Heronian triangle and the triple of the three lengths (a,b,c) is called a Heronian triple. For example, (13,14,15) is a Heronian triple. This triangle is composed of two Pythagorean triangles (5,12,13) and (9,12,15). There are also obtuse Heronian triangles, such as (4,13,15), which can be derived by removing (5,12,13) from (9,12,15).
Heronian Triangles (13,14,15) and (4,13,15)
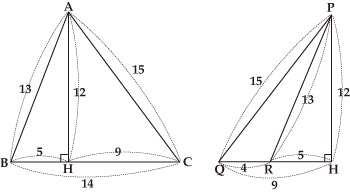 △ABC and △PQR are Heron triangles, with areas of 84 and 24 respectively.
△ABC and △PQR are Heron triangles, with areas of 84 and 24 respectively.
-


"Koukogen no seisu ken ken"
Lager image of Sanpo tenzan shinanroku
Sanpo tenzan shinanroku
Any Pythagorean triangle per se is a Heronian triangle, and combining two Pythagorean triangle in this way can produce a Heronian triangle. However, there are also Heronian triangles, such as (65,119,180), which cannot be produced by combining Pythagorean triangles. In this case, however, if we create a triangle (325,595,900) by multiplying each side with 5, this triangle is one that can be derived from combining two Pythagorean triangles, (91,312, 325) and (91,588,595). As indicated by this example, multiplying each side of a Heronian triangle with a natural number will produce a triangle which can be produced by combining two Pythagorean triangles.
Heronian triples consisting of three consecutive natural numbers, such as (13,14,15), include (51,52,53), (193,194,195) and so on, and indeed an infinite number of larger Heronian triangles exist. This example is demonstrated by Arima Yoriyuki (1714-1783) in his Shuuki sanpo(1769). In Wasan, Fujita Sadasuke (1734-1807) found the general Heronian triple in his Seiyo sanpo(1781).
-


Heronian Triple Consisting of Three Consecutive Natural Numbers
Library for Shuuki sanpo
Shuuki sanpo
NDL Digital Collections