Chapter 2. Seki Takakazu
Column Why does 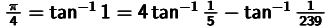 hold true? (Level 3)
hold true? (Level 3)
With respect to angle α, assume
![]() .
.
Then, we obtain
![]() .
.
By repeating this, we obtain
![]() .
.
And now, as
![]()
holds true due to
![]() ,
,
the Addition Theorem with respect to tan,
![]()
or
![]()
is derived.
J. Machin, an astronomer from London, discovered that
![]()
held true when
![]()
, and he calculated Pi to 100 decimal points in 1706 by using this relationship and
![]() .
.
When we actually calculate
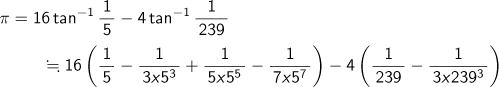
with an 8-digit calculator, we obtain a figure of 3.1415918.
Subsequently, relational expressions were discovered including the following:
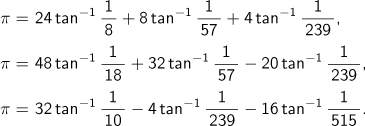
Using such expressions, calculations to evaluate Pi to still further decimal places were attempted.