Column Pi (Ratio of the Circumference of a Circle to Its Diameter)

Circles are all similar, and "the circumference divided by the diameter" produces the same value regardless of their radius. This value is the ratio of the circumference of a circle to its diameter and is called π (Pi). This constant appears in the calculation of the area of a circle, and is a type of an irrational number known as a transcendental number that can be expressed neither by a fraction nor by any radical sign such as a square root, nor their combination. The number has an infinite number of decimal places, namely, 3.1415926535..., and it has now been computed to 5 trillion decimal places by computers.

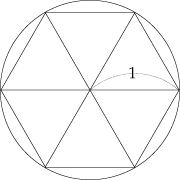$The circumference is greater than 6 from the figure. As the diameter of the circle is 2, Pi is greater than 3.$ The circumference is greater than 6 from the figure. As the diameter of the circle is 2, Pi is greater than 3.

$Pi, the First 10,000 Decimal Places Enshuritsu 1000000 Keta Hyo$
Pi, the First 10,000 Decimal Places
Enshuritsu 1000000 Keta Hyo
Enshuritsu 1000000 Keta Hyo

As for the value of π, ancient civilizations used their own. As a regular hexagon that is inscribed in a circle with a radius of 1 has a perimeter of 6, it is revealed that Pi has a value greater than 3. In the ancient Egypt, they obtained an approximation of

$256/81$ (approximately, 3.16)

by placing a regular octagon on a circle, and in ancient Babylonia they used

$3+1/8=3.125$ .

Archimedes came to the conclusion in his work Kyklu metresis (measure of a circle) that Pi satisfies

$3+10/71(=3.140845) <π < 3+1/7(=3.1428571)$ .

In ancient India, we can find an example of the use of $√10$ =3.1622776 or

$62832/20000=3.1416$ .

In China, they used

$142/45=3.15555$

$198/63=3.1428571$

$355/113=3.1415929$

for Pi.
In the Edo Period of Japan, Jinkoki (1627) by Yoshida Mitsuyoshi used 3.16 for Pi, but as people recognized that this value was not accurate, a field called Enri (en means a circle and ri means a theory), in which more accurate values for Pi were calculated, began to evolve. Wasan scholars such as Muramatsu Shigekiyo, Seki Takakazu, Kamata Toshikiyo, Takebe Katahiro, and Matsunaga Yoshisuke calculated more accurate values of Pi, and accomplished results that could be compared to European mathematics.

In Europe, Viete (1540-1603) discovered the first formula that expresses π:

$2/π=√(1/2) × √{(1/2)+(1/2)×√(1/2)}×√[(1/2)+(1/2)×√{(1/2)+(1/2)×√(1/2)}]×√...$

After that, the Wallis (1616-1703) Formula:

$π/2=(2×2×4×4×6×6×...)/(1×3×3×5×5×7×7×...)$

the Gregory (1638-1675) and Leibniz (1646-1716) Formula:

$π/4=1-1/3+1/5-1/7+1/9 ...$

Moreover, Newton (1642-1727) and Euler (1707-1783) discovered a series that converged faster, which enabled them to calculate values of Pi to more decimal places. If we use the relation

$π/4= Arctangent(1)=4 arctangent(1/5) - arctangent(1/239)$ discovered by J. Machin (1680-1752),

we can obtain a value of 3.14159 for π accurate to five decimal places with the first 4 terms of the Taylor expansion of tan^-1.In a recent computer calculation, the following equations were used:

$π=48 arctangent(1/49)-128 arctangent(1/57)-20 arctangent(1/239)+48 arctangent(1/110443)$

$π=176 arctangent(1/57)+28 arctangent(1/239)-48 arctangent(1/682)+96 arctangent(1/12943)$

* tan^-1 : Arc tangent. The inverse function of tangent.

Calculation of Pi in Wasan

At the end of Sanpo shojo, a method for calculating Pi appears. To summarize what is described in the book, the method is as follows: Assume the original number=3,

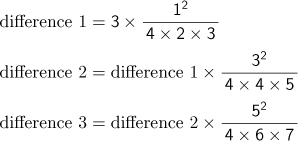
$difference 1=3×1^2/(4×2×3), difference 2=(difference 1)×3^2/(4×4×5), difference 3=(difference 2)x5^2/(4×6×7)$

Continue this until difference 100 is created. Then, Pi is derived by adding the original number, difference 1, difference 2, difference 3...and so on. Rewriting this as a mathematical expression, it is shown to have following regularity:

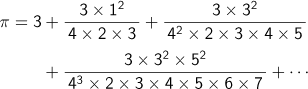
$π=3+3×(1^2)/(4×2×3)+3×3^2/(4^2×2×3×4×5)+3×3^2×5^2/(4^3×2×3×4×5×6×7)+...$

$'Kyu enshu hijutsu kigen' (Origin of secret art of finding Pi) from Sanpo shojo The book asserts that this method is a direct and clear solution to the calculation of Pi without using Kakujutsu or Kaiho (evolution), but does not explain why it is a formula for the calculation of π.$
"Kyu enshu hijutsu kigen" (Origin of secret art of finding Pi) from Sanpo shojo
The book asserts that this method is a direct and clear solution to the calculation of Pi without using Kakujutsu or Kaiho (evolution), but does not explain why it is a formula for the calculation of π.
NDL Digital Collections
Sanpo shojo

This formula is the same as the one described in Hoen sankei (1739)by Matsunaga Yoshisuke. The formation of this formula is also included in Koshigen koutei (1819) by Ninchou.

$'Kyushusu' from Hoen sankei Pi (for a circle with a diameter of 1) is calculated accurately to 49 decimal places.$
"Kyushusu" from Hoen sankei
Pi (for a circle with a diameter of 1) is calculated accurately to 49 decimal places.
NDL Digital Collections
Hoen sankei

In the Meiji Era, Kikuchi Dairoku released four English papers to introduce the calculation of Pi in Wasan in Tokyo sugaku butsuri gakkai kiji Vol. 7 (1896). In the first treatise, he introduced the calculation in Sanpo kyuseki tsuko (1844) by Hasegawa Hiromu, and explained Enrikatsujutsu, a type of calculus calculation, originally started by Wada Yasushi (1787-1840) with Western calculation formulae.

$'What is the area of a circle with a diameter of 1?' from Sanpo kyuseki tsuko. In this book, he obtains the area of a circle with a diameter of 1, and finds Pi by dividing the area by 4.$
" What is the area of a circle with a diameter of 1?" from Sanpo kyuseki tsuko
In this book,
he obtains the area of a circle with a diameter of 1, and finds Pi by dividing the area by 4. In this calculation,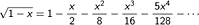 $√(1-x)=1-x/2-x^2/8-x^3/16-5x^4/128- ...$ is used.
NDL Digital Collections
Sanpo kyuseki tsuko

When incrementing n for $(r=1)Σn(r^i)$ (the sum of the powers of the natural numbers),

$(r=1)Σn(r^i)≒n^(i+1)/(i+1)$

holds true; Hasegawa uses this to obtain the result of

$π/4=1-1/(2×3)-1/(5×8)-1/(7×16)-5/(9×128)- ...$

We do not know anything about the number's regularity from this result alone. In fact, however, there is a relationship between the terms. Each term is decided by multiplying its previous term by a regular fraction as follows:

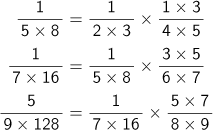
$1/(5×8)= 1/(2×3)×(1×3/4×5)、1/(7×16)= 1/(5×8)×(3×5/6×7)、5/(9×128)= 1/(7×16)×(5×7/8×9)$

Kikuchi noticed that such a series was what K. F. Gauss (1777-1855) named a hypergeometric series. A hypergeometric series is defined as follows:

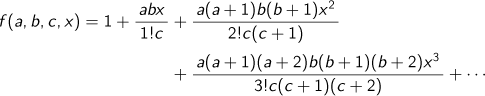
$f(a,b,c,x)=1+abx/1!c+a(a+1)b(b+1)x^2/2!c(c+1)+a(a+1)(a+2)b(b+1)(b+2)x^3/3!c(c+1)(c+2)+ ...$

Therefore, Kikuchi proved in the next paper that the calculation

$π=2(1+1/6+3/40+5/113+ ...)$

in Enri shinko by Wada Yasushi was equivalent to

$π=2f(1/2, 1/2, 3/2, 1)$

Hasegawa's calculation

$π/4=1-1/(2×3)-1/(5×8)-1/(7×16)-5/(9×128)- ...$

was equivalent to

$π/4=F(1/2, 3/2, 5/2, 1)/3$

and that Matsunaga's

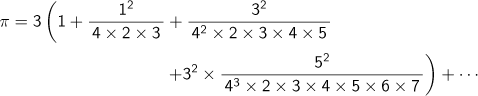
$π=3(1+1^2/(4×2×3)+3^2/(4^2×2×3×4×5)+3^2×5^2/(4^3×2×3×4×5×6×7)+...)$

was equivalent to

$π=3 F(1/2, 1/2, 3/2, 1/4)$ .

In Wasan, Seki Takakazu, Takebe Katahiro, etc., sought calculation formulas for π².

$π^2=9(1+1^2/(3×4)+(1^2×2^2)/(3×4×5×6)+(1^2×2^2×3^2)/(3×4×5×6×7×8)+ ...)$

, derived by Takebe, is the first formula to evaluate Pi in the history of Wasan. Takebe calculated π to 41 decimal places with this formula. In the next treatise, Kikuchi derived

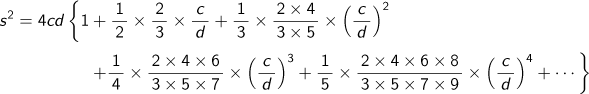
$s^2=4cd{1+ (1/2)×(2/3)×(c/d) + (1/3)×(2×4)/(3×5)×(c/d)^2 + (1/4)×(2×4×6)/(3×5×7)×(c/d)^3 + (1/5)×(2×4×6×8)/(3×5×7×9)×(c/d)^4 + ...}$

to express the square of s or the arc of a circle with sagitta c and diameter d, which was described by Yamaji Nushizumi in Kenkon no maki (c 1765), and proved

$π^2=8{1 + (1/2)×(2/3)×(1/2) + (1/3)×(2×4)/(3×5)×(1/2)^2 + (1/4)×(2×4×6)/(3×5×7)×(1/2)^3 + ...}=8{1 + (1/2)×(1/3) + (1/3)×(1×2)/(3×5) + (1/4)×(1×2×3)/(3×5×7) + ...}$

because

$s=dπ/2$

when

$c=d/2$ .

Arc, Sagitta, and Diameter of a Circle

$Arc, Sagitta, and Diameter of a Circle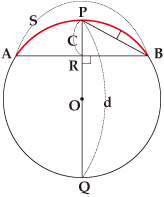$ In the figure, $APB$ ,a part of the circumference, is called ko (arc), the segment AB is called gen (chord), and the segment PR is ya (sagitta).The diameter PQ is called kei in Japanese.
When we draw a chord for the arc PB and a sagitta for the chord, and continue to repeat this process with shorter chords, the shape derived by connecting these chords approaches that of a circle. This way, Yamaji calculates s, the length of the arc, when the diameter is d and the length of the sagitta is c.

In the last paper, he proved that

$π/2=1+1/3+(1×2)/(3×5)+(1×2×3)/(3×5×7)+(1×2×3×4)/(3×5×7×9)+ ...$

derived by Ajima Naonobu in Kohai jutsukai could be simplified to

$π/2=F(1, 1, 3/2, 1/2)$

In the following year, Kikuchi also wrote a paper to introduce a method of calculating the length of an arc derived by Takebe Katahiro in Tokyo Sugaku Butsuri Gakkai Kiji Vol. 8 (1897). This set of papers was intended to introduce to the world the fact that theories he had found in calculations of Pi in Wasan were comparable to calculus in the West.

Chapter 2. Seki Takakazu

ColumnPi (Ratio of the Circumference of a Circle to Its Diameter) (Level 1)

Calculation of Pi in Wasan

Arc, Sagitta, and Diameter of a Circle