Chapter 3. Master Institution - Wasan as a Hobby
Column Sangaku (Mathematical Tablet) (Level 0)
Sangaku (mathematical tablet) refers to a tablet in the form of Ema (votive wooden tablet with a ridge in the form of a roof on which a horse is painted), in which a mathematical problem was described. The tablet was dedicated to shrines and temples in the Edo period. Many of the problems in Sangaku dealt with beautiful geometrical figures, most of which were colored. The oldest existing Sangaku is the one dedicated to the Hoshinomiya Shrine in present day Sano City in Tochigi Prefecture in the third year of Tenna (1683). This original Sangaku, however, caught fire in 1975 and was rendered illegible, so its duplicate is now displayed. The second oldest Sangaku was one dedicated to the Yasaka Shrine in Kyoto in the fourth year of Genroku (1691), and was designated as the Important cultural properties of Japan in 1993. The custom of Sangaku is said to have flourished in the Edo period, and continued to exist until the Meiji era. However, since the Meiji era, the habit had fallen into disuse and the posted Sangaku were removed due to reasons such as damage, and it is said that the number of existing tablets is now about 1,000 (the number of those from the Edo period is about 400).
No perfect record remains to inform us how many mathematical tablets were actually made, and we only can perceive from books in which mathematical tablets were reproduced what kinds of mathematical tablets were dedicated. It is said that the first book that mentioned mathematical tablets was Sanpo futsudankai (1673)by Murase Gieki, which described the mathematical tablets posted in Meguro Fudo. The first book that collected mathematical tablets was Shinpeki sanpo by Fujita Sadasuke (1734-1807), which was published in the first year of Kansei (1789). In the eighth year of Kansei (1796), the augmented edition was published under the title Zokoku shinpeki sanpo ge, and in the fourth year of Bunka (1807), Fujita's son Fujita Yoshitoki (1772-1828) published Zoku shinpeki sanpo as its sequel. They mainly recorded mathematical tablets created by Fujita's disciples. Saishi shinsan (1830)(1830) by Nakamura Tokikazu (?-1881), which was disseminated in the form of handwritten copy only, recorded 204 mathematical tablets.
In the Edo period, there were so-called itinerant Wasan scholars who taught Wasan while they were traveling across the country. One such scholar, Yamaguchi Kazu (c.1781-1850), left a record of such tours he made from the fourteenth year of Bunka (1817) to the eleventh year of Bunsei (1824), called Dochu nikki. In the book, he transcribed 324 problems from mathematical tablets he saw across the country. In addition, there were many handwritten duplicate copies left that recorded mathematical tablets dedicated to individual shrines.
In the Meiji era, Wasan came to be studied as a subject of mathematical history rather than a field that was applicable to real problems. Wasan research was started by deciphering Wasan books, and some researchers focused on mathematical tablets left around the country.The first book compiled from examining mathematical tablets left across the country in the prewar period was Shaji hono sangaku shu(1942) by Shimizu Yoshio (1896-1983), which included 141 mathematical tablets. As only 68 copies of the book were published in stencil printing, they are hard to obtain.
In the postwar period, investigations began to be conducted on mathematical tablets left all over the country. Hirayama Akira (1904-1998), a Wasan researcher, published the results from investigating mathematical tablets left in Yamagata, Fukushima, and Chiba in the 1960's. Then, collections of mathematical tablets in Nagano, Ibaraki, Niigata, Saitama, and Tochigi were published indivisually. Shimodaira Kazuo (1928-1994), a Wasan researcher, created a list of the whereabouts of 817 existing mathematical tablets as an appendix to the new version of Bunkashijo yori mitaru nihon no sugaku (1984) by Mikami Yoshio. It was Fukagawa Hidetoshi (1943-), who investigated mathematical tablets in Aichi starting from the 1970's, that succeeded this work, and he created a list of 884 existing mathematical tablets and 91 restored ones in Reidai de shiru nihon no sugaku to sangaku (1998). In addition, he also created a list of 1,749 mathematical tablets that no longer exist but can be confirmed through literature. In 2005, Nagoya City Science Museum held the "Exhibition of Common People's Arithmetic," which collected about 130 mathematical tablets. Note that you can see pictures of the mathematical tablets at the homepage called "Wasan Hall"( http://www.wasan.jp/ )
Mathematical tablets have beautiful figures drawn on them, and many of the problems included in them have answers in simple expressions, and as the books by Fukagawa Hidetoshi have been published in English, overseas Sangaku lovers are increasing in number. In France, a book about Sangaku called Sangaku; le mystere des enigmes geometriques japonaises (Paris, 2008)by G. Huvent has been published.There are also domestic publications such as Japanese temple mathematical problems in Nagano Pref. Japan (Nagano City, 2003), introducing Sangaku in English.
Recently, many novels focusing on Wasan have been written, often featuring the story of Sangaku. For example, a novel titled Sanpo shojo (1973) by Endo Hiroko, a juvenile literature writer, whose subject is adopted from the book with the same title, begins from the moment when the lead character finds that a solution to a problem in a Sangaku is wrong.
Problem in Sangaku that Appears in Sanpo shojo by Endo Hiroko
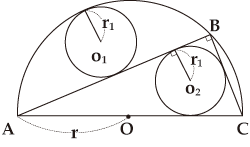 In the figure, △ABC is a right triangle inscribed in a semi-circle having a radius of r with O as its center; the circles O1 and O2 have the same radius of r1, O1is the largest circle that is tangential to the arc
In the figure, △ABC is a right triangle inscribed in a semi-circle having a radius of r with O as its center; the circles O1 and O2 have the same radius of r1, O1is the largest circle that is tangential to the arc
![]() and the segment AB; and O2 is the circle inscribed within △ABC. Then, this question seeks to determine the relationship between r and r1.
and the segment AB; and O2 is the circle inscribed within △ABC. Then, this question seeks to determine the relationship between r and r1.
The problems in Sangaku include many geometric problems such as this, and a collection of formulae like Sanpo jojutsu(1841) by Yamamoto Kazen (1811-?), which assembles beautiful relationships in terms of mathematics, has been created.
-

Shinpeki sanpo
Lager image of Shinpeki sanpo -
Zoku shinpeki sanpo
Lager image of Zoku shinpeki sanpo -

Problem in Mathematical Tablet in the Asakusa Kanzeondo
Lager image of Saishi shinsan
Saishi shinsan