幾何の問題 解答
容術
| A9 | コラム「測量の方法」 にあったヘロンの公式と面積の関係では、三角形の3辺の長さをa,b,c、面積をS、内接円の半径をrとする時、
という簡単な式となります。 |
|---|
| A10 |
|
|---|
| A11 | 図で△ABCは直角三角形ですので (1) a2+b2=(2R)2です。Q9 の結果を使うと、内接円の半径は (2) |
|---|
裁ち合せ
| A12 |
|
|---|
| A13 |
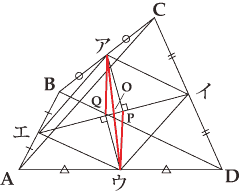 図の点ア、イ、ウ、エはそれぞれ各辺の中点ですので、四角形アイウエは平行四辺形になります(線分アイと線分ウエはともに共通の線分BDと平行で長さがその半分、線分アエと線分イウはともに共通の線分ACと平行で長さがその半分ですので、線分アイと線分ウエは平行で長さが等しく、同じように線分アエと線分イウは平行で長さが等しい)。したがって、線分アウと線分イエはそれぞれの中点で交わり、その交点をOとします。次に、線分イエに対して点アと点ウから垂線をおろし、その足をそれぞれP、Qとします。すると線分アPと線分ウQは平行で、線分アO=線分ウOですので、四角形アPウQは平行四辺形となります。これより、線分アP=線分ウQ、線分PO=線分QOとなり、従って線分エQ=線分イP、 線分エP=線分イQとなっています。四角形の内角の和は360°ですので、イエ、アP、ウQを切って、下図のように並べ変えると、きれいに長方形になります。また、この長方形の面積は「イエ×アP×2」となります。 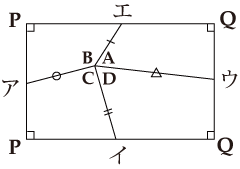
|
|---|



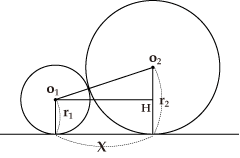 図の直角三角形O1O2Hにピタゴラスの定理を使い、(r2-r1)2+x2=(r1+r2)2より x2=4r1r2 、すなわち
図の直角三角形O1O2Hにピタゴラスの定理を使い、(r2-r1)2+x2=(r1+r2)2より x2=4r1r2 、すなわち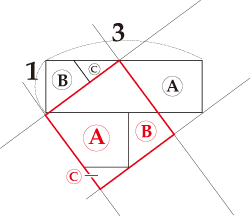 面積1の正方形を3個並べた長方形の面積は3ですので、作りたい正方形の1辺の長さは
面積1の正方形を3個並べた長方形の面積は3ですので、作りたい正方形の1辺の長さは
