コラムヘロンの公式

三角形の3辺の長さがわかると面積を計算できます。3辺の長さがa,b,cである時、この三角形の面積は $s=(a+b+c)/2$ とすると $S=√s(s-a)(s-b)(s-c)$ となります。この証明は次のように行います。

三角形の面積

$三角形の面積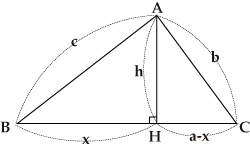$ 3辺の長さがa,b,cの三角形の面積を求めるには、Aから辺BCへ垂線をたらし、その足をHとしてAH=hとおきます。△ABCの面積は $S=(1/2)ah$ ですが、ahをa,b,cだけの式に直すと、ヘロンの公式となります。

図で、h²=c²-x²=b²-(a-x)²、従って c²-x²=b²-a²+2ax-x²　から

$x=(c2+a2-b2)/2a$

となります。
すると

$h2=c2-(c2+a2-b2)2/(2a)2$

より

4a²h²=4a²c²-(c²+a²-b²)²
=(2ac+c²+a²-b²)(2ac-c²-a²+b²)={(c+a)²-b²}{b²-(c-a)²}
=(c+a+b)(c+a-b)(b+c-a)(b-c+a)

ここで a+b+c=2s とおくと、　4a²h²=2s(2s-2b)(2s-2a)(2s-2c)=16s(s-a)(s-b)(s-c)
すなわちa²h²=4s(s-a)(s-b)(s-c)　から　 $ah=2√s(s-a)(s-b)(s-c)$

ところで $S=ah/2$ なので、 $S=√s(s-a)(s-b)(s-c)$ となります。

この式を使うと、3辺とも自然数である三角形の面積を容易に計算することができます。コラム「ピタゴラスの定理」にあるように、この三角形の面積も自然数となる時、ヘロン三角形と呼ばれます。3辺の長さが(4,13,15), (3,25,26), (9,10,17), (7,15,20), (6,25,29), (11,13,20), (5,29,30), (13,14,15)などの三角形はヘロン三角形となりますので、この公式を使って確かめてみてください。

三角形の内接円の半径

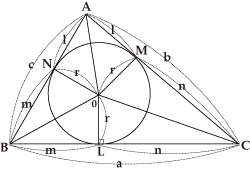$三角形の内接円の半径$ 図のように3辺の長さがa,b,cの三角形ABCにOを中心とする半径rの円が内接しています。この時、Oは内心と呼ばれ、△AMO≡△ANO、△BNO≡△BLO、△CLO≡△CMOとなります。

3辺の長さがわかると、内接円の半径を計算できます。図で△ANO≡△AMO, △CMO≡△CLO,
△BLO≡△BNOですので、

$S=2×(rl/2+rm/2+rn/2)=r(l+m+n)$

となりますが、a+b+c=2(l+m+n)
ですので、

$S=r(a+b+c)/2=rs$

となります。従って、ヘロンの公式より

$r=√{(s-a)(s-b)(s-c)/s}$

となります。
最後に円に内接する四角形の面積の公式を書いておきます。

円に内接する四角形の面積

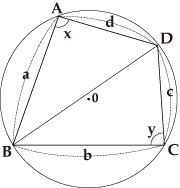$円に内接する四角形の面積$ 内接四角形の性質x+y=180°と△ABDの面積が $(1/2)$ ad sin x、△BCDの面積が $(1/2)$ bc sin yとなることを利用し、また余弦定理を使ってBD²を2通りに表わすと、全体の面積の式からsin x、sin yなどを消去することができます。

図のように４辺の長さをa,b,c,dとすると、 $s=(a+b+c+d)/2$ とおくと、四角形ABCDの面積は $S=√(s-a)(s-b)(s-c)(s-d)$ となります。証明は頑張って挑戦してみてください。ちなみにCとDが重なるとd=0の三角形となり、ヘロンの公式そのものとなります。

第4章実学としての和算