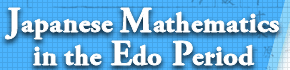Chapter 4. Wasan as a Practical Science
Column Heron’s Formula (Level 1)
The area of a triangle can be calculated when the lengths of its three sides are found. Assuming that the area of a triangle is S and let
![]() where a, b, and c are the lengths of the three sides of the triangle, then it follows that
where a, b, and c are the lengths of the three sides of the triangle, then it follows that
![]() . The formula can be proved as follows:
. The formula can be proved as follows:
Area of a Triangle
 To find the area of a triangle with three sides whose lengths are a, b, and c, drop the perpendicular from A to the side BC, let the foot of the perpendicular be H and assume AH=h. The area of △ABC is
To find the area of a triangle with three sides whose lengths are a, b, and c, drop the perpendicular from A to the side BC, let the foot of the perpendicular be H and assume AH=h. The area of △ABC is ![]() , and if we represent ah using a, b, and c only, we obtain Heron’s formula.
, and if we represent ah using a, b, and c only, we obtain Heron’s formula.
Looking at the figure, we know that 、h2=c2-x2=b2-(a-x)2 holds true, and therefore we obtain
![]()
from c2-x2=b2-a2+2ax-x2.
Then, using
![]()
it follows that
4a2h2=4a2c2-(c2+a2-b2)2
=(2ac+c2+a2-b2)(2ac-c2-a2+b2)={(c+a)2-b2}{b2-(c-a)2}
=(c+a+b)(c+a-b)(b+c-a)(b-c+a)
Here, letting a+b+c=2s, we obtain 4a2h2=2s(2s-2b)(2s-2a)(2s-2c)=16s(s-a)(s-b)(s-c).
Therefore, ![]() is derived from
a2h2=4s(s-a)(s-b)(s-c).
is derived from
a2h2=4s(s-a)(s-b)(s-c).
On the other hand, as ![]() , we obtain
, we obtain
![]() .
.
Using this formula, we can easily calculate the area of any triangle with the lengths of the sides of which are all represented with natural numbers. As described in Column "Pythagorean theorem", when the area of this triangle is also a natural number, it is called a Heronian triangle. Triangles whose three sides are (4,13,15), (3,25,26), (9,10,17), (7,15,20), (6,25,29), (11,13,20), (5,29,30), (13,14,15) and so on, are Heronian triangles; please confirm this using Heron’s formula.
Radius of the Inscribed Circle of a Triangle
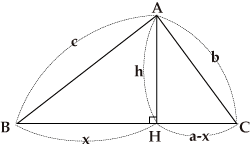
 As shown in the figure, a circle with a radius of r with O as its center is inscribed within the triangle ABC with three sides of lengths a, b, and c respectively. In this case, O is called the inner center, and it follows that △AMO≡△ANO, △BNO≡△BLO, and △CLO≡△CMO.
As shown in the figure, a circle with a radius of r with O as its center is inscribed within the triangle ABC with three sides of lengths a, b, and c respectively. In this case, O is called the inner center, and it follows that △AMO≡△ANO, △BNO≡△BLO, and △CLO≡△CMO.
The radius of the inscribed circle of a triangle can be calculated when the lengths of its three sides are found. From the figure, it follows that △ANO≡△AMO, △CMO≡△CLO and △BLO≡△BNO.So, we obtain
![]() ;
;
as a+b+c=2(l+m+n) , we obtain
![]() .
.
Therefore, we obtain
![]()
by Heron’s formula.
Finally, let us present the formula for calculating the inscribed quadrangle of a circle.
Area of the Inscribed Quadrangle of a Circle
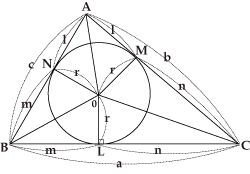
 Using the fact that x+y=180° or a property of the inscribed quadrilateral, and the area of △ABD is
Using the fact that x+y=180° or a property of the inscribed quadrilateral, and the area of △ABD is ![]() ad sin x, and the area of △BCD is
ad sin x, and the area of △BCD is ![]() bc sin y, and representing BD2 in two ways using the law of cosines, we can eliminate sin x, sin y, etc., from the expression of the total area.
bc sin y, and representing BD2 in two ways using the law of cosines, we can eliminate sin x, sin y, etc., from the expression of the total area.
As shown by the figure, assuming the lengths of the four sides are a, b, c, d, and letting ![]() , the area of the quadrangle ABCD is
, the area of the quadrangle ABCD is ![]() .
We would like you to try to prove the formula. For your reference:
.
We would like you to try to prove the formula. For your reference:
If C and D overlap, the quadrangle becomes a triangle with d=0 and the formula changes to Heron’s formula itself.